（本小题满分13分）已知圆
C：
过点A（3，1），且过点P（4，4）的直线PF与圆C相切并和x轴的负半轴相交于点F．
（1）求切线PF的方程；
（2）若抛物线E的焦点为F,顶点在原点，求抛物线E的方程。
（3）若Q为抛物线E上的一个动点，求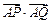
的取值范围．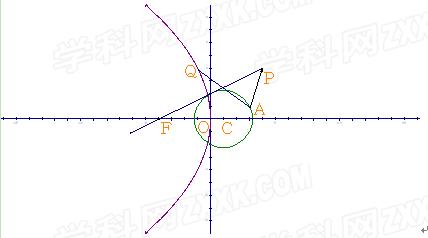
已知函数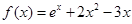
．
（1）求证函数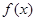
在区间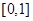
上存在唯一的极值点，并用二分法求函数取得极值时相应
的近似值（误差不超过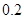
）；（参考数据
，
，
）
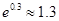（2）当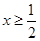
时，若关于的不等式
恒成立，试求实数
的取值范围.
设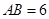
，在线段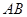
上任取两点（不含两端点），将线段分成了三条线段．
（1）若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形的概率；
（2）若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形的概率．
如图，三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，DE垂直平分线段PC，且分别交AC、PC于D、E两点,又PB=BC，PA=AB。
（1）求证：PC⊥平面BDE；
（2）若点Q是线段PA上任一点，判断BD、DQ的位置关系，并证明你的结论；
（3）若AB=2,求三棱锥B-CED的体积
已知函数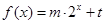
的图像经过点A(0，0)，B(3，7)及C
，
为数列
的前n项和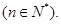
（I）求
（II）若数列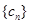
满足
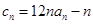，求数列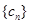的前n项和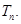
在△ABC中，内角A，B，C所对边长分别为
，
，
，
.
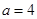（1）求
的最大值及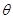
的取值范围；
（2）求函数
的最大值和最小值.