(本小题满分 12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
(I)设所选5人中女医生的人数为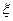 ,求
,求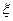
 的分布列及数学期望;
的分布列及数学期望;
(II)现从10名医生中的张强、李军、王刚、赵永4名男医生,李莉、孙萍2名女医生共6人中选一正二副3名组长,在张强被选中的情况下,求李莉也被选中的概率.
(
在区间[0,1]上给定曲线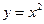 ,
, 轴.
轴.
(1)当面积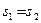 时,求P点的坐标。
时,求P点的坐标。
(2)试在此区间确定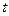 的值,使
的值,使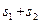 的值最小,并求出最小值。
的值最小,并求出最小值。
已知向量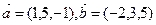 .
.
(1)若
(2)若
(1)当实数 取何值时,复数
取何值时,复数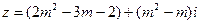 在复平面内对应的点
在复平面内对应的点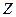 在直线
在直线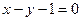 上?
上?
(2)已知 ,如果
,如果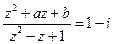 ,求实数
,求实数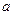 和
和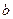 的值。
的值。
(本小题满分14分)
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求f(x)的解析式;
(2)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(3)若当x=1时,函数y=g(x)取得极值,确定y=g(x)的单调区间.
(本小题满分13分)
已知双曲线C: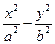 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为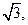 焦点到渐近线的距离为
焦点到渐近线的距离为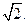
(1)求双曲线C的方程;
(2)已知直线x-y+m =0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
=0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
线y2="4" x上,求m的值.