(
在区间[0,1]上给定曲线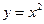 ,
, 轴.
轴.
(1)当面积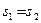 时,求P点的坐标。
时,求P点的坐标。
(2)试在此区间确定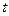 的值,使
的值,使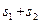 的值最小,并求出最小值。
的值最小,并求出最小值。
(本小题满分12分)
随着国家政策对节能环保型小排量车的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注.已知2011年1月Q型车的销量为 辆,通过分析预测,若以2011年1月为第1月,其后两年内Q型车每月的销量都将以1%的
辆,通过分析预测,若以2011年1月为第1月,其后两年内Q型车每月的销量都将以1%的 增长率增长,而R型车前
增长率增长,而R型车前 个月的销售总量
个月的销售总量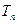 满足关系式:
满足关系式:
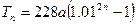
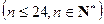 .
.
(Ⅰ)求Q型车前 个月的销售总量
个月的销售总量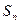 的表达式;
的表达式;
(Ⅱ)比较两款车前 个月的销售总量
个月的销售总量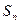 与
与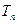 的大小关系;
的大小关系;
(本小题满分12分)
如图(1)是一正方体的表面展开图,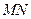 和
和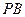 是两条面对角线,请在图(2)的正方体中将
是两条面对角线,请在图(2)的正方体中将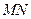 和
和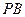 画出来,并就这个正方体解决下面问题.
画出来,并就这个正方体解决下面问题.
(Ⅰ)求证: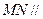 平面
平面 ;
;
(Ⅱ)求证: ⊥平面
⊥平面 ;
;
(Ⅲ)求二面角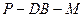 的大小.
的大小.
(本小题满分12分)
为了构建和谐社会建立幸福指标体系,某地决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 相关人员数 |
抽取人数 |
|
| 公务员 |
32 |
 |
| 教师 |
48 |
 |
| 自由职业者 |
64 |
4 |
(Ⅰ)求研究小组的总人数;
(Ⅱ)若从研究小组的公务员和教师中随机选2人撰写研究报告,求其中恰好有1人来自公务员的概率.
(本小题满分12分)
如图,设 是单位圆和
是单位圆和 轴正半轴的交点,
轴正半轴的交点,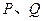 是单位圆上的两点,
是单位圆上的两点,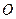 是坐标原点,
是坐标原点, ,
,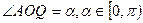 .
.
(Ⅰ)若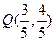 ,求
,求 的值;
的值;
(Ⅱ)设函数 ,求
,求 的值域.
的值域.
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为ξ,求随机变量ξ的分布列.