(本小题满分14分)已知函数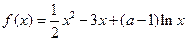 ,
,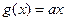 ,
,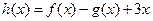 ,其中
,其中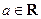 且
且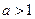 .
.
(I)求函数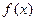 的导函数
的导函数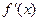 的最小值;
的最小值;
(II)当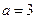 时,求函数
时,求函数 的单调区间及极值;
的单调区间及极值;
(III)若对任意的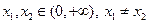 ,函数
,函数 满足
满足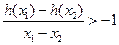 ,求实数
,求实数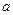
的取值范围 .
.
(本小题12分)定义在定义域D内的函数 ,若对任意的
,若对任意的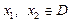 都有
都有 ,则称函数
,则称函数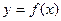 为“妈祖函数”,否则称“非妈祖函数”.试问函数
为“妈祖函数”,否则称“非妈祖函数”.试问函数 ,
,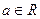 )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.


(本小题满分12分)某港口海水的深度 (米)是时间
(米)是时间 (时)(
(时)( )的函数,记为:
)的函数,记为:
已知某日海水深度的数据如下:
 (时) (时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 (米) (米) |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察, 的曲线可近似地看成函数
的曲线可近似地看成函数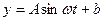 的图象
的图象
 (1)试根据以上数据,求出函数
(1)试根据以上数据,求出函数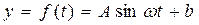 的振幅A、最小正周期T和表达式;
的振幅A、最小正周期T和表达式; (2)一般情况下,船舶航行时,船底离海底的距离为
(2)一般情况下,船舶航行时,船底离海底的距离为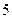 米或
米或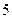 米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为
米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为 米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)?
米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)?
(本小题满分12分)已知函数 有最大值
有最大值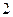 ,试求实数
,试求实数 的值.
的值.
(本小题满分12分)设函数 .
.
(1)写出 的最大值M,最小值m,最小正周期T;
的最大值M,最小值m,最小正周期T;
(2)试求最小正整数k,使得当自变量x在任意两个整数间(包括整数本身)变化时,函数 至少有一个值是M和一个值是m .
至少有一个值是M和一个值是m .
(本小题满分12分)
某市地铁全线共有四个车站,甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”。
号车站下车”。
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率。