(本小题满分14分)设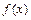 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,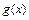 的图象与
的图象与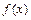 的图象关于直线
的图象关于直线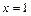 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,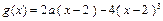 222233.
222233.
(1)求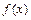 的解析式;
的解析式;
(2)若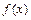 在
在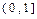 上为增函数,求
上为增函数,求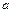 的取值范围;
的取值范围;
(3)是否存在正整数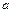 ,使
,使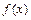 的图象的最高点落在直线
的图象的最高点落在直线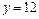 上?若存在,求出
上?若存在,求出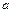 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分16分)
已知函数f(x)=x2-x+t,t≥0,g(x)=lnx.
(1)令h(x)=f(x)+g(x),求证:h(x)是增函数;
(2)直线l与函数f(x),g(x)的图象都相切.对于确定的正实数t,讨论直线l的条数,并说明理由.
(本小题满分16分)
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线
l:x=m+1与x轴的交点为B,BF2=m. 
(1)已知点(,1)在椭圆C上,求实数m的值;
(2)已知定点A(-2,0).
①若椭圆C上存在点T,使得=,求椭圆C的离心率的取值范围;
②当m=1时,记M为椭圆C上的动点,直线AM,BM分别与椭圆C交于另一点P,Q,
若=λ,=m,求证:λ+m为定值.
(本小题满分14分)
如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记ÐAOP=q,q∈(0,π).
(1)当q=时,求点P距地面的高度PQ;
(2)试确定q的值,使得ÐMPN取得最大值.
(本小题满分14分)
在四棱锥P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E为PA的中点.
(1)求证:BE∥平面PCD;
(2)求证:平面PAB⊥平面PCD.
(本小题满分14分)
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.