(本小题满分16分)
已知函数f(x)=x2-x+t,t≥0,g(x)=lnx.
(1)令h(x)=f(x)+g(x),求证:h(x)是增函数;
(2)直线l与函数f(x),g(x)的图象都相切.对于确定的正实数t,讨论直线l的条数,并说明理由.
已知函数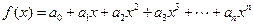 (n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(2)当n为奇函数时,设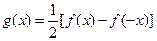 ,是否存在自然数m和M,使不等式m<
,是否存在自然数m和M,使不等式m<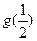 <M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
<M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
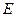 、
、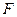 是椭圆
是椭圆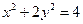 的左、右焦点,
的左、右焦点,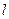 是椭圆的右准线,点
是椭圆的右准线,点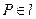 ,过点
,过点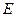 的直线交椭圆于
的直线交椭圆于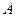 、
、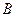 两点.(1)当
两点.(1)当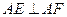 时,求
时,求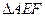 的面积;(2)当
的面积;(2)当 时,求
时,求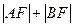 的大小;(3)求
的大小;(3)求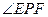 的最大值.
的最大值.
(本小题满分12分)如图,已知直三棱柱ABC—A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. (Ⅰ)求异面直线AB和C1D所成的角(用反三角函数表示);(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D; 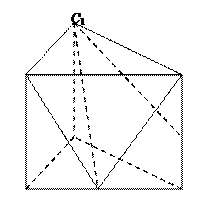
(Ⅲ)在(Ⅱ)的条件下,求点D到平面B1C1E的距离.
有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各学校做问卷调查.某中学A,B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分为:5、8、9、9、9;B班5名学生得分为:6,7,8,9,10.
(1)请你估计A,B两个班中哪个班的问卷得分要稳定一些;
(2)如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率.
(本小题满分12分)已知函数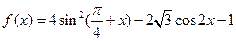 ,且给定条件
,且给定条件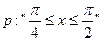 .
.
⑴求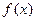 的最大值及最小值;
的最大值及最小值;
⑵若又给条件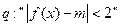 ,且
,且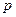 是
是 的充分条件,求实数
的充分条件,求实数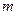 的取值范围。
的取值范围。