已知函数y=f(x)对任意的实数ab都有:f(a+b)=f(a)+f(b)﹣1,且x>0时,f(x)>1,
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,求f(2)的值,并解不等式f(3m2﹣m﹣2)<3.
已知f(x)=ax3+bx2+cx(a≠0)在x=1和x=-1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试求f(x) 的单调区间;
(3) 试判断x=±1时函数取极小值还是极大值,并说明理由.
已知某长方体的棱长之和为14.8m,长方体底面的一边比另一边长0.5m,问高为多少时长方体体积最大?并求出最大体积是多少?
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)-mf(x)在[-1,1]上是增函数,求实数m的取值范围.
已知集合A={x|x≥|x2-2x|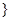 ,B={x|
,B={x|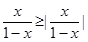 },C={x|ax2+x+b<0
},C={x|ax2+x+b<0 ,
,
(1)求A∪B,A∩B
(2)如果(A∪B)∩C=φ,A∪B∪C=R,求实数a、b的值.