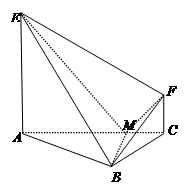.(本小题满分12分)
如图,在四梭锥中S-ABCD中,AB上AD,AB∥CD,CD=3AB=3,平面SAD上平面ABCD,E是线段AD上一点,AE=ED=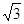 ,SE⊥AD.
,SE⊥AD.
(I)证明:平面SBE⊥平面SEC,
(Ⅱ)若SE=1.求三棱锥E-SBC的高。
从某校高三年级800名学生中随机抽取50名测量身高.据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果分成八组得到的频率分布直方图如下: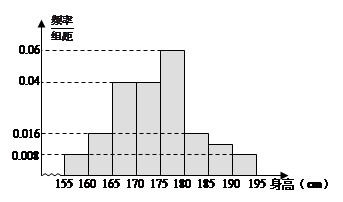
(1)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少;
(2)在样本中,若学校决定身高在185cm以上的学生中随机抽取2名学生接受某军校考官进行面试,求:身高在190cm以上的学生中至少有一名学生接受面试的概率.
(本小题满分13分)
设函数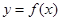 对任意的实数
对任意的实数 ,都有
,都有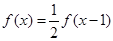 ,且当
,且当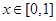 时,
时,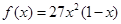 。
。
(1)若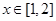 时,求
时,求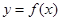 的解析式;
的解析式;
(2)对于函数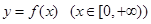 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点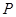 ,使得函数在点
,使得函数在点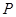 处的切线与
处的切线与 平行。若存在,那么这样的点
平行。若存在,那么这样的点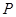 有几个;若不存在,说明理由。
有几个;若不存在,说明理由。
(3)已知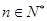 ,且
,且 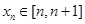 ,记
,记 ,求证:
,求证: 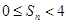 。
。
(本小题满分13分)
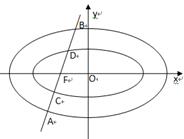
已知椭圆
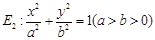 .
.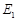 与
与 有相同的离心率,过点
有相同的离心率,过点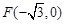 的直线
的直线 与
与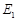 ,
, 依次交于A,C,D,B四点(如图).当直线
依次交于A,C,D,B四点(如图).当直线 过
过 的上顶点时, 直线
的上顶点时, 直线 的倾斜角为
的倾斜角为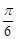 .
.
(1)求椭圆 的方程;
的方程;
(2)求证: ;
;
(3)若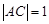 ,求直线
,求直线 的方程.
的方程.
(本小题满分13分)
平地上有一条水渠,其横断面是一段抛物线弧,如图,已知渠宽为
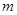 ,渠深为6
,渠深为6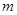 。
。
(1)若渠中水深为4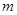 ,求水面的宽,并计算水渠横断面上的过水面积;
,求水面的宽,并计算水渠横断面上的过水面积;
(2)为了增大水渠的过水量,现要把这条水渠改挖(不能填土)成横断面为等腰梯形的水渠,使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽。
(本小题满分12分)
如图, 是直角三角形,
是直角三角形,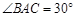 ,
, 交
交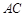 于点
于点 ,
,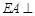 平面
平面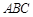 ,
,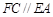 ,
,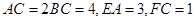 .
.
(1)证明: ;
;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.