在直角坐标系xOy中,椭圆C1: 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: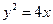 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
·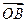 =0,求直线l的方程.
=0,求直线l的方程.
已知集合 ,
, .
.
(1)求集合 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
已知集合A={-4,2 -1,
-1, },B={
},B={ -5,1-
-5,1- ,9},分别求适合下列条件的
,9},分别求适合下列条件的 的值.
的值.
(1) ;
;
(2) .
.
已知函数 在[0,+∞)上是减函数,试比较
在[0,+∞)上是减函数,试比较 与
与 的大小.
的大小.
已知 为函数
为函数 图象上一点,
图象上一点, 为坐标原点,记直线
为坐标原点,记直线 的斜率
的斜率 .
.
(1)若函数 在区间
在区间 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;
(2)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求证:
已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点 ,点
,点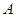 是曲线
是曲线 在第一象限的交点,且
在第一象限的交点,且 .
.
(1)求双曲线 的方程;
的方程;
(2)以双曲线 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆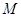 与直线
与直线 相切,圆
相切,圆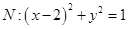 .过点
.过点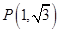 作互相垂直且分别与圆
作互相垂直且分别与圆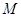 、圆
、圆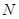 相交的直线
相交的直线 和
和 ,设
,设 被圆
被圆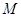 截得的弦长为
截得的弦长为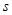 ,
, 被圆
被圆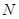 截得的弦长为
截得的弦长为 ,问:
,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.