已知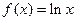
，
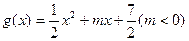，直线
与函数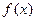
的图象相切，切点的横坐标为
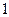，且直线与函数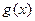
的图象也相切.（Ⅰ）求直线的方程及实数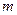
的值；（Ⅱ）若
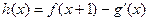(其中
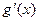是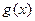的导函数)，求函数
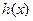的最大值；（Ⅲ）当
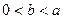时，求证：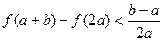
（本题满分12分.）
数列中｛an｝，a1=8，a4=2，且满足an+2= 2an+1- an，
（1）求数列｛an｝的通项公式；
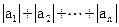（2）设Sn=
，求Sn
（本题满分12分.）已知26列货车以相同的速度v由A地驶向相距400千米远的B地，
每两列货车间的距离为d千米，现知d与v速度的平方成正比，且当v=20，d=1.
(1) 写出d关于v的函数解析式式及定义域；
（2）若不计货车的长度，则26列货车都到达B地至少需要多少小时？此时货车速度为多少？
（本题满分12分.）在锐角三角形中，边a，b是方程
的两根，
角A，B满足
，求角C的度数，边c的长度及三角形ABC的面积
等差数列｛an｝不是常数列，a5=10， a5, a7 a10是某个等比数列的｛bn｝的第1,3,5项。
（1）求数列｛an｝的第20项
（2）求数列｛bn｝的通项公式
已知
，解关于x的不等式