如图,在△ABO中,已知点 、B(﹣1,﹣1)、C(0,0),正比例函数y=﹣x图象是直线l,直线AC∥x轴交直线l与点C.
、B(﹣1,﹣1)、C(0,0),正比例函数y=﹣x图象是直线l,直线AC∥x轴交直线l与点C.
(1)C点的坐标为 (﹣3,3) ;
(2)以点O为旋转中心,将△ABO顺时针旋转角α(90°<α<180°),使得点B落在直线l上的对应点为B′,点A的对应点为A′,得到△A′OB′.
①∠α= 90° ;②画出△A′OB′.
(3)写出所有满足△DOC∽△AOB的点D的坐标.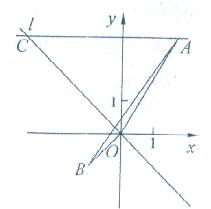
一个正方形的边长增加3cm,它的面积就增加39cm2,这个正方形的边长是多少?
作图题有公路 同侧、
同侧、 异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路
异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路 、
、 的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法)。
的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法)。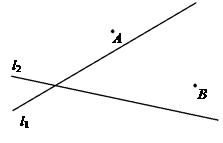
(1)先化简,再求值: ,其中a=3。
,其中a=3。
(2)解方程:
(1)计算题:(每题4分,共8分)
①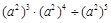
②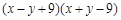
(2)因式分解(每题4分,共8分)
①
②
(本小题10分)如图,已知数轴上有A、B、C三个点,它们表示的数分别是18,8,﹣10.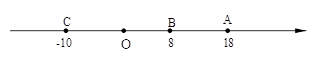
(1)填空:AB=___________,BC="_________" ;
(2)若点A以每秒1个单位长度的速度向右运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向左运动.试探索:BC﹣AB的值是否随着时间t的变化而改变?请说明理由.
(3)现有动点P、Q都从A点出发,点P以每秒1个单位长度的速度向终点C移动;当点P移动到B点时,点Q才从A点出发,并以每秒3个单位长度的速度向左移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,试用含t的代数式表示P、Q两点间的距离.