(本小题10分)如图,已知数轴上有A、B、C三个点,它们表示的数分别是18,8,﹣10.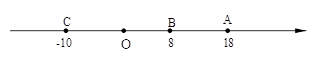
(1)填空:AB=___________,BC="_________" ;
(2)若点A以每秒1个单位长度的速度向右运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向左运动.试探索:BC﹣AB的值是否随着时间t的变化而改变?请说明理由.
(3)现有动点P、Q都从A点出发,点P以每秒1个单位长度的速度向终点C移动;当点P移动到B点时,点Q才从A点出发,并以每秒3个单位长度的速度向左移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,试用含t的代数式表示P、Q两点间的距离.