我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例。如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了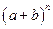
（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律。例如，在三角形中第三行的三个数1，2，1，恰好对应
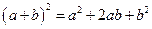展开式中的系数;第四行的四个数1，3，3，1，恰好对应着
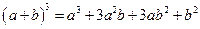展开式中的系数等等。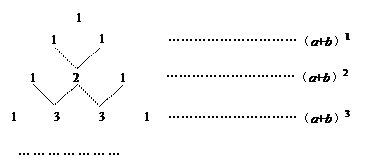
（1）根据上面的规律，写出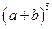
的展开式。
（2）利用上面的规律计算：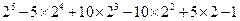
（1）先化简，再求值：
，其中
；
（2）已知
，求代数式
的值.
计算：（1）
（2）
（3）
（4）
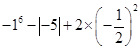
A、B两地果园分别有苹果
吨和
吨，C、D两地分别需要苹果
吨和
吨；已知从A、B到C、D的运价如下表：
（1）若从A果园运到C地的苹果为
吨，则从A果园运到D地的苹果为吨，从A果园将苹果运往D地的运输费用为元；
（2）用含的式子表示出总运输费．
“十·一”黄金周期间，某市风景区在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）：
（1）请判断七天内游客人数最多的是哪天？最少的是哪天？它们相差多少万人？
（2）若9月30日的游客人数为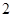
万人，求这7天的游客总人数是多少万人？
某厂家生产的产品按订货商的要求需要按图示的三种打包方式中的一种进行打包．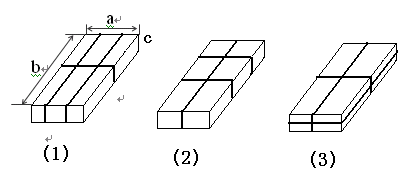
（1）请用代数式分别表示三种打包方式的绳子长度；
（2）若厂家为节省绳子，则请直接写出所选用的打包方式？（其中
）．