(10分)如图1,O为正方形ABCD的中心,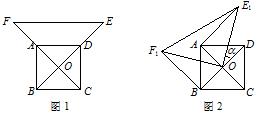
分别延长OA、OD到点F、E,使OF=2OA,
OE=2OD,连接EF.将△EOF绕点O逆时针
旋转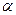 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当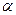 =30°时,求证:△AOE1为直角三角形.
=30°时,求证:△AOE1为直角三角形.
化简:
在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒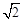 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.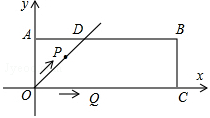
(1)当点P移动到点D时,求出此时t的值;
(2)当t为何值时,△PQB为直角三角形;
(3)已知过O、P、Q三点的抛物线解析式为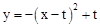 (t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
“五•一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.
(1)求a的值.
(2)求检票到第20分钟时,候车室排队等候检票的旅客人数.
(3)若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?
【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.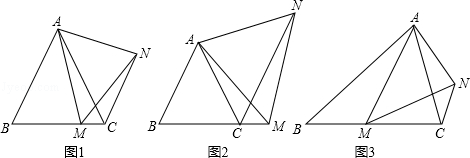
据《2012年衢州市国民经济和社会发展统计公报》(2013年2月5日发布),衢州市固定资产投资的相关数据统计图如下: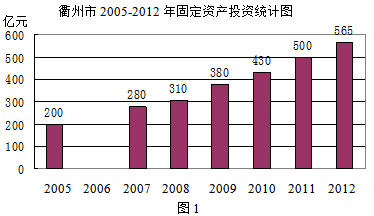
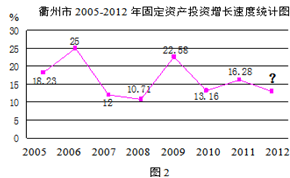
根据以上信息,解答下列问题:
(1)求2012年的固定资产投资增长速度(年增长速度即年增长率);
(2)求2005﹣2012年固定资产投资增长速度这组数据的中位数;
(3)求2006年的固定资产投资金额,并补全条形图;
(4)如果按照2012年的增长速度,请预测2013年衢州市的固定资产投资金额可达到多少亿元(精确到1亿元)?