（年贵州省贵阳市）如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．
（1）求MP的值；
（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？
（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）
计算: 
已知
是方程组
的解，试求
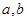的值。
小虎一家利用元旦三天驾车到某景点旅游，小汽车出发前油箱有油36L，匀速行驶若干小时后，油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示，根据图象回答下列问题：
（1）求油箱余油量Q与行驶时间t之间的函数关系式；
（2）如果出发地距景点200km，车速为80km/h，要到达景点，油箱中的油是否够用？请说明理由．
如图，在矩形纸片ABCD中，AB=6，BC=8．把△BCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点G；E、F分别是C′D和BD上的点，线段EF交AD于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．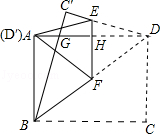
（1）求证：△ABG≌△C′DG；
（2）求tan∠ABG的值；
（3）求EF的长．
如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，∠CBA=32°，求∠EFD的度数。