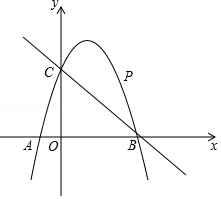
如图,已知二次函数 的图象经过点 ,与 轴分别交于点 ,点 .点 是直线 上方的抛物线上一动点.
(1)求二次函数 的表达式;
(2)连接 , ,并把 沿 轴翻折,得到四边形 .若四边形 为菱形,请求出此时点 的坐标;
(3)当点 运动到什么位置时,四边形 的面积最大?求出此时 点的坐标和四边形 的最大面积.
在图11的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1. 并写出点B的对应点B2的坐标;
△OAB内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标
判断△OA2B2能否看作是由△O1A1B1经过某种变换后得到的图形,若是,请指出是怎样变换得到的(直接写答案)
如图10,一艘轮船从离A观察站的正北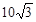 海里处的B港出发向东航行,观察站第一次测得该船在A地北偏东30°的C处;半小时后,又测得该船在A地的北偏东60°的D处,求此船的速度.
海里处的B港出发向东航行,观察站第一次测得该船在A地北偏东30°的C处;半小时后,又测得该船在A地的北偏东60°的D处,求此船的速度.
袋子中装有2个红球,1个黄球,它们除颜色外其余都相同. 小明和小张做摸球游戏,约定一次游戏规则是:小张先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小张赢,否则小明赢.请用树状图或列表格法表示一次游戏中所有可能出现的结果
这个游戏规则对双方公平吗?请说明理由.
某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个;定价每增加1元,销售量将减少10个.商店若准备获利2000元,则售价应定为多少?这时应进货多少个?
计算:cos30°
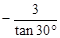 ;
;解方程: x(x+3)=2x+1