在图11的方格纸中，△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3)，△O1A1B1与△OAB是关于点P为位似中心的位似图形.
在图中标出位似中心P的位置，并写出点P及点B的对应点B1的坐标；
以原点O为位似中心，在位似中心的同侧画出△OAB的一个位似△OA2B2，使它与△OAB的相似比为2:1. 并写出点B的对应点B2的坐标；
△OAB内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标
判断△OA2B2能否看作是由△O1A1B1经过某种变换后得到的图形，若是，请指出是怎样变换得到的（直接写答案）
（本小题满分9分）如图，在平面直角坐标系中有Rt△ABC，∠A＝90°，AB＝AC，A（－2，0）、B（0，d）、C（－3，2）．
（1）求d的值；
（2）将△ABC沿
轴的正方向平移a个单位，在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上．请求出这个反比例函数和此时直线
的解析式；
（3）在（2）的条件下，直线交y轴于点G，作
⊥轴于
．
是线段上的一点，若△
和△
面积相等，求点坐标．
（本小题满分8分）为进一步弘扬祖国优秀传统文化，历下区教育局主办了“‘首善奖’历下区青少年书法大赛”．某校有2位同学获得一等奖，3位同学获得二等奖，随机抽取获奖同学谈谈他们的参赛体会．
（1）抽取一位同学谈体会，请直接写出该同学是二等奖获得者的概率；
（2）抽取两位同学谈体会，求两位同学分别是一等奖和二等奖获得者的概率．（用树状图或列表法求解）
应用题分式方程（本小题满分8分）
我区某校九年级的同学利用清明假期外出踏青、赏春．从学校到景区共10千米，一部分同学骑自行车先出发，10分钟后，其余同学乘汽车出发，结果他们同时到达集合地点．已知汽车的速度是骑车同学速度的2倍，求两部分同学分别每小时走多少千米？
（本小题满分7分）
（1）如图，四边形ABCD、四边形AEFD是平行四边形．求证：△ABE≌△DCF．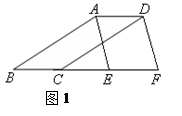
（2）如图，CB是⊙O的直径，P是CB延长线上一点，PB=2，PA切⊙O于A点，PA=4．求⊙O的半径．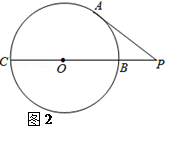
（本小题满分7分）
（1）计算：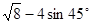
；
（2）解不等式组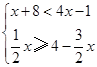
．