(本小题满分9分)如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
(1)求d的值;
(2)将△ABC沿 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线 的解析式;
的解析式;
(3)在(2)的条件下,直线 交y轴于点G,作
交y轴于点G,作 ⊥
⊥ 轴于
轴于 .
. 是线段
是线段 上的一点,若△
上的一点,若△ 和△
和△ 面积相等,求点
面积相等,求点 坐标.
坐标.
如图, 内接于 , 是 的直径,弦 与 交于点 ,连接 ,过点 作直线 ,使 .
(1)求证:直线 是 的切线.
(2)若 , , ,求 的长.

如图,建筑物 的高为52米,在其正前方广场上有人进行航模试飞.从建筑物顶端 处测得航模 的俯角 ,同一时刻从建筑物的底端 处测得航模 的仰角 ,求此时航模 的飞行高度.(精确到1米)
(参考数据: , ,

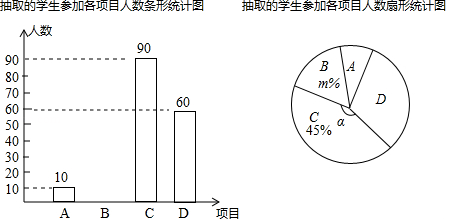
为加强未成年人思想道德建设.某校在学生中开展了“日行一孝”活动.活动设置了四个爱心项目: 项 我为父母过生日, 项 我为父母洗洗脚, 项 我当一天小管家, 项 我与父母谈谈心,要求每个学生必须且只能选择一项参加.为了解全校参加各项目的学生人数,随机抽取了部分学生进行调查,根据调查结果,绘制成如下两幅不完整的统计图,请根据所给信息,解答下列问题:
(1)这次抽样调查的样本容量是 ,补全图1中的条形统计图.
(2)在图2的扇形统计图中, 项所占的百分比为 ,则 的值为 , 项所在扇形的圆心角 的度数为 度.
(3)该校参加活动的学生共1200人,请估计该校参加 项的学生有多少人?
在创建“文明校园”活动中,某校有2名男生和3名女生被评为学校“文明学生”.现要从这5名学生中选拔“学校文明礼仪值周岗”的值周生.
(1)从这5名学生中随机选拔1人值周,恰好选到男生的概率是 .
(2)从这5名学生中随机选拔2人值周,请用树状图或列表法求出恰好选到1个男生和1个女生的概率.
如图, 与 是等边三角形,连接 ,取 的中点 ,连接 并延长至点 ,使 ,连接 , , ,将 绕点 顺时针旋转.
(1)如图1,当点 在 上,点 在 上时,则 的形状为 ;
(2)将 绕点 顺时针旋转至图2的位置,请判断 的形状,并说明理由;
(3)若 ,将 由图1位置绕点 顺时针旋转 ,当 时,请直接写出 的值.
