应用题分式方程(本小题满分8分)
我区某校九年级的同学利用清明假期外出踏青、赏春.从学校到景区共10千米,一部分同学骑自行车先出发,10分钟后,其余同学乘汽车出发,结果他们同时到达集合地点.已知汽车的速度是骑车同学速度的2倍,求两部分同学分别每小时走多少千米?
如图,等腰直角 中,
中, ,点
,点 在
在 上,将
上,将 绕顶点
绕顶点 沿顺时针方向旋
沿顺时针方向旋 后得到
后得到 .
.
求
 的度数
的度数当
 ,
, 时,求
时,求 的长
的长
已知关于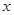 的方程
的方程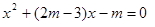 的两个不相等的实数根为
的两个不相等的实数根为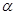 、
、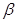 满足
满足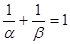 ,求
,求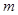 的值.
的值.
如图,数轴上点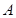 表示的数为
表示的数为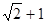 ,点
,点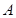 在数轴上向左平移
在数轴上向左平移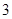 个单位到达点
个单位到达点 ,点
,点 表示的数为
表示的数为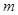 .
.
求
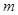 的值
的值化简:
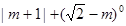
如图,直线 与
与 轴交于
轴交于 ,与
,与 轴交于
轴交于 ,以
,以 为边作矩形
为边作矩形 ,点
,点 在
在 轴上,双曲线
轴上,双曲线 经过点
经过点 与直线
与直线 交于
交于 ,
, 轴于
轴于 ,则
,则 .
.
如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。①当点
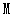 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点 、
、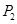 ,则
,则 (,)、
(,)、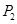 (,);②当∠OMN=60°时,对应的点P是点
(,);②当∠OMN=60°时,对应的点P是点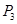 ,求
,求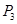 的坐标;
的坐标;若抛物线
 ,是经过(1)中的点
,是经过(1)中的点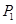 、
、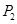 、
、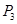 ,试求a、b、c的值;
,试求a、b、c的值;在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用
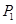 、
、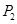 、
、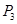 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.