(10分)如图1，O为正方形ABCD的中心，
分别延长OA、OD到点F、E，使OF＝2OA，
OE＝2OD，连接EF．将△EOF绕点O逆时针
旋转
角得到△E1OF1(如图2)．
(1)探究AE1与BF1的数量关系，并给予证明；
(2)当＝30°时，求证：△AOE1为直角三角形．
计算下列各题（每题4分，共32分）
⑴-20+（-14）-（-18）-13⑵ 10+（-2）×（-5）2
（3）
÷
-
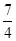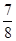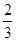×（-6）（4）（-
-
+
）÷（-
）
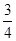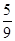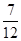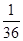（5）∣-
∣÷（-
）-
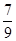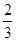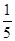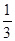×（-4）2（6）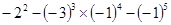
（7）
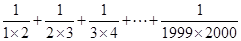(8) 
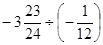
在数轴上表示下列各数，并用“<”连接：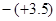 
，
， 
， 
，
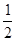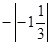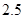
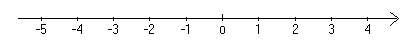
有一块直角三角形的绿地，量得两直角边长分别为3m，4m现在要将绿地扩充成等腰三角形，且扩充部分是以4m为直角边的直角三角形，求扩充后等腰三角形绿地的周长．
如图，在矩形ABCD中，E、F分别是边BC、AB上的点，且EF＝ED，EF⊥ED．试说明AE平分∠BAD．
如图，一张长方形纸片宽AB＝8 cm，长BC＝10 cm．现将纸片折叠，使顶点D落在BC边上的点F处(折痕为AE)，求EC的长．