计算下列各题(每题4分,共32分)
⑴-20+(-14)-(-18)-13 ⑵ 10+(-2)×(-5)2
(3)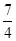 ÷
÷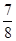 -
-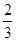 ×(-6) (4)(-
×(-6) (4)(-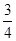 -
-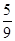 +
+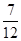 )÷(-
)÷(-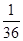 )
)
(5)∣-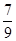 ∣÷(
∣÷(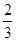 -
-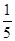 )-
)-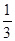 ×(-4)2 (6)
×(-4)2 (6)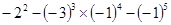
(7)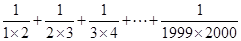 (8)
(8) 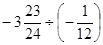
已知关于 的一元二次方程 .
(1)求证:无论 为何实数,方程总有两个不相等的实数根;
(2)若方程的两个实数根 , 满足 ,求 的值.
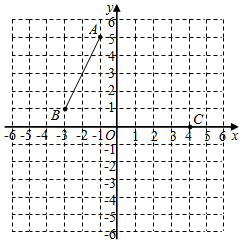
如图,在平面直角坐标系中,已知点 , 和 ,请按下列要求画图并填空.
(1)平移线段 ,使点 平移到点 ,画出平移后所得的线段 ,并写出点 的坐标为 ;
(2)将线段 绕点 逆时针旋转 ,画出旋转后所得的线段 ,并直接写出 的值为 ;
(3)在 轴上找出点 ,使 的周长最小,并直接写出点 的坐标为 .
有4张看上去无差别的卡片,上面分别写有数 ,2,5,8.
(1)随机抽取一张卡片,则抽取到的数是偶数的概率为 ;
(2)随机抽取一张卡片后,放回并混在一起,再随机抽取一张,请用画树状图或列表法,求抽取出的两数之差的绝对值大于3的概率.
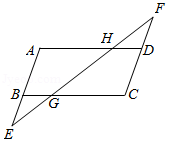
如图,在 中,点 在 的延长线上,点 在 的延长线上,满足 .连接 ,分别与 , 交于点 , .
求证: .
计算: .