小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1,时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式: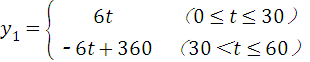
请你完成:
(1)求出图3中y2与t的函数关系式;
(2)直接写出A、B两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一个小时,请你在题图3中补全图象.
小明去博物馆参观,听到一段对话:
管理员:先生,这块化石有700 003年.
参观者:哇!你怎么知道这么精确?
管理员:3年前,几位考古学家到这参观,他们说这块化石有70万年了,3年过去了,所以是700 003年.
请问:管理员的推断对吗?为什么?
下列各数是由四舍五入得到的近似数,问:各精确到哪一位,各有哪几个有效数字?
(1)30亿;(2)1.20×105;(3)0.02050;(4)17.68;(5)37;(6)8.90.
下列由四舍五入得到的近似数,各精确到哪一位?
(1)1.300; (2)1.12×104; (3)12.5亿.
如图,一次函数y=-2x+t的图象与x轴,y轴分别交于点C,D.
(1)求点C,点D的坐标;
(2)已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点, 若以点C,点D为直角顶点的△PCD与△OCD相似。求t的值及对应的点P的坐标.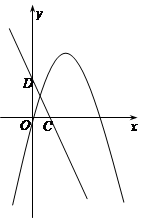
如图一,在Rt△ABC中,∠ACB=90°,∠A=30°,P为BC边上任意一点,点Q为AC边动点,分别以Cm、MQ为边做等边△MPF和等边△PQE,连接EF.
(一)试探索EF与AB位置关系,并证明;
(5)如图5,当点P为BC延长线上任意一点时,(一)结论是否成立?请说明理由.
(3)如图3,在Rt△ABC中,∠ACB=90°,∠A=m°,P为BC延长线上一点,点Q为AC边动点,分别以CP、PQ为腰做等腰△PCF和等腰△PQE,使得PC=PF,PQ=PE,连接EF.要使(一)的结论依然成立,则需要添加怎样的条件?为什么?