已知∠AOB=60°,半径为3cm的⊙P沿边OA从右向左平行移动,与边OA相切的切点记为点C.
(1)⊙P移动到与边OB相切时(如图),切点为D,求劣弧的长;
(2)⊙P移动到与边OB相交于点E,F,若EF=4cm,求OC的长;
如图,在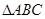 中,点
中,点 是
是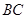 上的一点,且
上的一点,且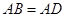 ,
,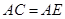 ,
, .求证:
.求证: .
.
先化简,再求值: ,其中
,其中 .
.
如图,在平面直角坐标系中,抛物线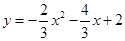 与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.
与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.
(1)填空:点A的坐标为(,),点B的坐标为(,),点C的坐标为(,),点D的坐标为(,);
(2)点P是线段BC上的动点(点P不与点B、C重合)
①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;
②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;
③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C重合),请直接写出△PQR周长的最小值.
如图,在▱ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将▱ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.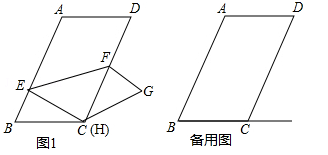
(1)当点H与点C重合时.
①填空:点E到CD的距离是;
②求证:△BCE≌△GCF;
③求△CEF的面积;
(2)当点H落在射线BC上,且CH=1时,直线EH与直线CD交于点M,请直接写出△MEF的面积.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90°,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.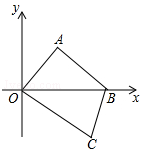
(1)求点A和点C的坐标;
(2)当0<t<30时,求m关于t的函数关系式;
(3)当m=35时,请直接写出t的值;
(4)直线l上有一点M,当∠PMB+∠POC=90°,且△PMB的周长为60时,请直接写出满足条件的点M的坐标.