已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD =  ,求a的值.
,求a的值.

如图①,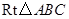 中,
中,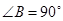 ,
,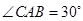 .它的顶点
.它的顶点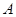 的坐标为
的坐标为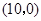 ,顶点
,顶点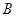 的坐标为
的坐标为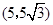 ,
,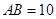 ,点
,点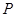 从点
从点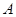 出发,沿
出发,沿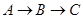 的方向匀速运动,同时点
的方向匀速运动,同时点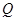 从点
从点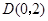 出发,沿
出发,沿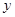 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点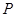 到达点
到达点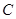 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为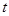 秒.
秒.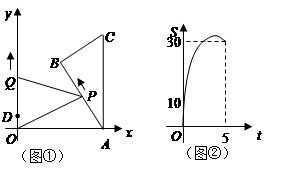
(1)求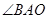 的度数.
的度数.
(2)当点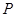 在
在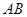 上运动时,
上运动时,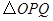 的面积
的面积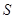 (平方单位)与时间
(平方单位)与时间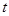 (秒)之间的函数图象为抛物线的一部分,(如图②),求点
(秒)之间的函数图象为抛物线的一部分,(如图②),求点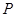 的运动速度.
的运动速度.
(3)求(2)中面积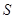 与时间
与时间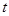 之间的函数关系式及面积
之间的函数关系式及面积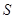 取最大值时点
取最大值时点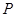 的坐标.
的坐标.
(4)如果点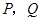 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点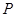 沿
沿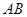 边运动时,
边运动时,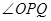 的大小随着时间
的大小随着时间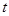 的增大而增大;沿着
的增大而增大;沿着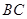 边运动时,
边运动时,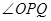 的大小随着时间
的大小随着时间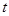 的增大而减小,当点
的增大而减小,当点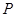 沿这两边运动时,使
沿这两边运动时,使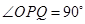 的点
的点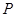 有几个?请说明理由.
有几个?请说明理由.
通过市场调查,一段时间内某地区某一种农副产品的需求数量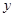 (千克)与市场价格
(千克)与市场价格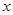 (元/千克)(
(元/千克)(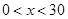 )存在下列关系:
)存在下列关系:
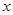 (元/千克) (元/千克) |
5 |
10 |
15 |
20 |
 (千克) (千克) |
4500 |
4000 |
3500 |
3000 |
又假设该地区这种农副产品在这段时间内的生产数量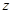 (千克)与市场价格
(千克)与市场价格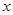 (元/千克)成正比例关系:
(元/千克)成正比例关系: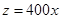 (
(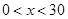 ).现不计其它因素影响,如果需求数量
).现不计其它因素影响,如果需求数量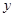 等于生产数量
等于生产数量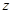 ,那么此时市场处于平衡状态.
,那么此时市场处于平衡状态.
(1)请通过描点画图探究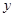 与
与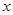 之间的函数关系,并求出函数关系式;
之间的函数关系,并求出函数关系式;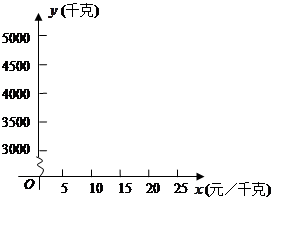
(2)根据以上市场调查,请你分析:当市场处于平衡状态时,该地区这种农副产品的市场价格与这段时间内农民的总销售收入各是多少?
(3)如果该地区农民对这种农副产品进行精加工,此时生产数量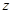 与市场价格
与市场价格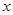 的函数关系发生改变,而需求数量
的函数关系发生改变,而需求数量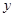 与市场价格
与市场价格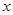 的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?
的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?
某学校七年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.
(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.
(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规完:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.
(3)在(2)的游戏规则下,让小军从最外环进口任意进入10次,最终小张和小李的总得分之和不超过28分,请问小军至少几次进入迷宫中心?
2007年5月17日我市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向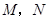 两地之间修建一条道路.已知:如图
两地之间修建一条道路.已知:如图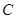 点周围180m范围内为文物保护区,在
点周围180m范围内为文物保护区,在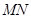 上点
上点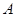 处测得
处测得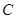 在
在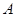 的北偏东
的北偏东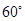 方向上,从
方向上,从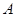 向东走500m到达
向东走500m到达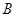 处,测得
处,测得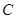 在
在 的北偏西
的北偏西 方向上.
方向上.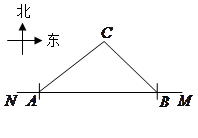
(1)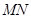 是否穿过文物保护区?为什么?(参考数据:
是否穿过文物保护区?为什么?(参考数据: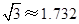 )
)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
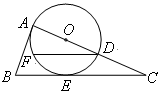
已知:如图,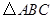 中,
中,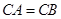 ,点
,点 为
为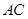 的中点,以
的中点,以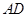 为直径的
为直径的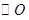 切
切 于点
于点 ,
,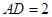 .
.
(1)求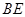 的长;(2)过点
的长;(2)过点 作
作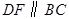 交
交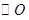 于点
于点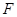 ,求
,求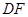 的长.
的长.