某学校七年级数学兴趣小组组织一次数学活动．在一座有三道环形路的数字迷宫的每个进口处都标记着一个数，要求进入者把自己当做数“1”，进入时必须乘进口处的数，并将结果带到下一个进口，依次累乘下去，在通过最后一个进口时，只有乘积是5的倍数，才可以进入迷宫中心，现让一名5岁小朋友小军从最外环任一个进口进入．
（1）小军能进入迷宫中心的概率是多少？请画出树状图进行说明．
（2）小组两位组员小张和小李商量做一个小游戏，以猜测小军进迷宫的结果比胜负．游戏规则规完：小军如果能进入迷宫中心，小张和小李各得1分；小军如果不能进入迷宫中心，则他在最后一个进口处所得乘积是奇数时，小张得3分，所得乘积是偶数时，小李得3分，你认为这个游戏公平吗？如果公平，请说明理由；如果不公平，请在第二道环进口处的两个数中改变其中一个数使游戏公平．
（3）在（2）的游戏规则下，让小军从最外环进口任意进入10次，最终小张和小李的总得分之和不超过28分，请问小军至少几次进入迷宫中心？
现有两个不透明的乒乓球盒，甲盒中装有1个白球和2个红球，乙盒中装有2个白球和若干个红球，这些小球除颜色不同外，其余均相同．若从乙盒中随机摸出一个球，摸到红球的概率为
．
（1）求乙盒中红球的个数；
（2）若先从甲盒中随机摸出一个球，再从乙盒中随机摸出一个球，请用树形图或列表法求两次摸到不同颜色的球的概率．
为迎接中招体育加试，需进一步了解九年级学生的身体素质，体育老师随机抽取九年级一个班共50名学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，图表如下图所示：请根据图表信息完成下列问题：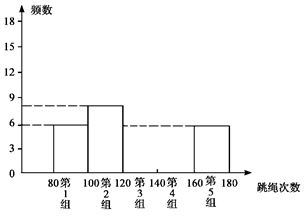
（1）直接写出表中a的值；
（2）请把频数分布直方图补充完整；
（3）若在一分钟内跳绳次数少于120次的为测试不合格，则该班学生进行一分钟跳绳不合格的概率是多少？
如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连接CE．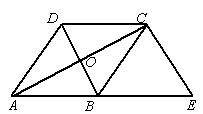
（1）求证：BD=EC；
（2）若∠E=50°，求∠BAO的大小．
解方程：①
②
③先化简：
，并从0，
，2中选一个合适的数作为
的值代入求值．
在平面直角坐标系中，O为坐标原点，点A坐标为（1，0），以OA为边在第一象限内作等边△OAB，C为x轴正半轴上的一个动点（OC＞1），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．
（1）如图，当C点在x轴上运动时，设AC＝x，请用x表示线段AD的长；
（2）随着C点的变化，直线AE的位置变化吗？若变化，请说明理由；若不变，请求出直线AE的解析式．
（3）以线段BC为直径作圆，圆心为点F，
①当C点运动到何处时直线EF∥直线BO？此时⊙F和直线BO的位置关系如何？请说明理由．
②G为CD与⊙F的交点，H为直线DF上的一个动点，连结HG、HC，求HG＋HC的最小值，并将此最小值用x表示．