某课题研究小组就图形面积问题进行专题研究，他们发现如下结论：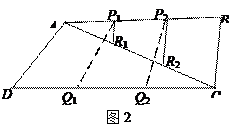
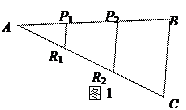
（1）有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比；
（2）有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比；
…
现请你继续对下面问题进行探究，探究过程可直接应用上述结论．（S表示面积）
问题1：如图1，现有一块三角形纸板ABC，P1，P2三等分边AB，R1，R2三等分边AC．
经探究知
＝
S△ABC，请证明．
问题2：若有另一块三角形纸板，可将其与问题1中的拼合成四边形ABCD，如图2，Q1，Q2三等分边DC．请探究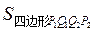
与S四边形ABCD之间的数量关系．
问题3：如图3，P1，P2，P3，P4五等分边AB，Q1，Q2，Q3，Q4五等分边DC．若
S四边形ABCD＝1，求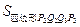
．
问题4：如图4，P1，P2，P3四等分边AB，Q1，Q2，Q3四等分边DC，P1Q1，P2Q2，P3Q3
将四边形ABCD分成四个部分，面积分别为S1，S2，S3，S4．请直接写出含有S1，S2，S3，S4的一个等式．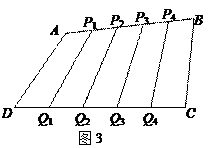
先化简，再求值： 
，其中
若关于x的二次函数y=a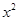
+bx+c（a＞0，c＞0，a、b、c是常数）与x轴交于两个不同的点A（
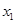，0），B（
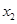，0）（0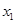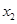＜＜），与y轴交于点P，其图像顶点为点M，点O为坐标原点。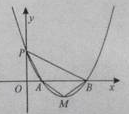
（1）当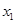=c=2，a=
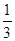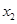时，求与b的值；
（2）当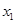=2c时，试问△ABM能否为等边三角形？判断并证明你的结论；
（3）当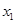=mc（m＞0）时，记△MAB，△PAB的面积分别为S1，S2，若△BPO∽△PAO，且S1=S2,求m的值。
|
在直角坐标系中，我们不妨将横坐标，纵坐标均为整数的点称之为“中国结”。
（1）求函数y=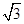
x+2的图像上所有“中国结”的坐标；
（2）求函数y=
（k≠0，k为常数）的图像上有且只有两个“中国结”，试求出常数k的值与相应“中国结”的坐标；
（3）若二次函数y=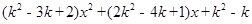
（k为常数）的图像与x轴相交得到两个不同的“中国结”，试问该函数的图像与x轴所围成的平面图形中（含边界），一共包含有多少个“中国结”？
如图，在直角坐标系中，⊙M经过原点O（0,0），点A（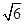
，0）与点B（0，－
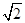），点D在劣弧OA上，连接BD交x轴于点C，且∠COD=∠CBO。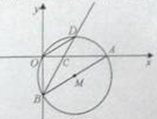
（1）求⊙M的半径；
（2）求证：BD平分∠ABO；
（3）在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标。
现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件。现假定该公司每月的投递总件数的增长率相同：
（1）求该快递公司投递快递总件数的月平均增长率；
（2）如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？