(本小题满分12分)已知各项均为正数的数列 中,
中, 是数列
是数列 的前
的前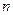 项和,对任意
项和,对任意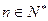 ,有
,有 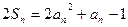 .函数
.函数 ,数列
,数列 的首项
的首项 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令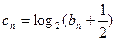 求证:
求证: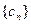 是等比数列并求
是等比数列并求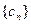 通项公式;
通项公式;
(Ⅲ)令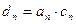 ,
, ,求数列
,求数列 的前n项和
的前n项和 .
.
B(文)设 是定义在
是定义在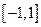 上的偶函数,当
上的偶函数,当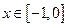 时,
时,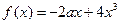 222233.
222233.
(1)若 在
在 上为增函数,求
上为增函数,求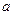 的取值范围;
的取值范围;
(2)是否存在正整数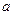 ,使
,使 的图象的最高点落在直线
的图象的最高点落在直线 上?若存在,求出
上?若存在,求出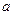 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)A(理)已知函数 ,其中
,其中 .
.
(1)若存在 ,使得
,使得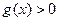 成立,求实数
成立,求实数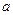 的取值范围;
的取值范围;
(2)求函数 的值域.
的值域.
(本小题满分12分)某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数 与听课时间
与听课时间 之间的关系满足如图所示的曲线.当
之间的关系满足如图所示的曲线.当 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当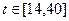 式,曲线是函数
式,曲线是函数 (
( 且
且 )图象的一部分.根据专家研究,当注意力指数
)图象的一部分.根据专家研究,当注意力指数 大于等于80时听课效果最佳.
大于等于80时听课效果最佳.
(1) 试求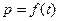 的函数关系式;
的函数关系式;
(2) 老师在什么时段内安排核心内容能使得学生听课效果最佳?请说明理由.
(本小题满分12分)在 中,内角
中,内角 的对边长分别为
的对边长分别为 ,
,
且 成等差数列,
成等差数列,
(1)若 成等比数列,试判断
成等比数列,试判断 的形状;
的形状;
(2)若 ,求
,求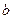 .
.
(本小题满分12分)已知函数
(1)求函数 的最值与最小正周期;
的最值与最小正周期;
(2)求使不等式 )成立的
)成立的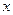 的取值范围.
的取值范围.