数学课上,李老师出示了这样一道题目:如图 ,正方形
,正方形 的边长为
的边长为 ,
, 为边
为边 延长线上的一点,
延长线上的一点, 为
为 的中点,
的中点, 的垂直平分线交边
的垂直平分线交边 于
于 ,交边
,交边 的延长线于
的延长线于 .当
.当 时,
时, 与
与 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过 作直线平行于
作直线平行于 交
交 ,
, 分别于
分别于 ,
, ,如图
,如图 ,则可得:
,则可得: ,因为
,因为 ,所以
,所以 .可求出
.可求出 和
和 的值,进而可求得
的值,进而可求得 与
与 的比值.
的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
如图,在平面直角坐标系 中,过点 的直线 与直线 相交于点 .
(1)求直线 的表达式;
(2)过动点 且垂直于 轴的直线与 , 的交点分别为 , ,当点 位于点 上方时,写出 的取值范围.

关于 的一元二次方程 有两个不相等的实数根.
(1)求 的取值范围;
(2)写出一个满足条件的 的值,并求此时方程的根.
如图,四边形 是平行四边形, 平分 ,交 的延长线于点 .求证: .

设抛物线的解析式为 ,过点 作 轴的垂线,交抛物线于点 ;过点 , 作 轴的垂线,交抛物线于点 ; ;过点 , 为正整数)作 轴的垂线,交抛物线于点 ,连接 ,得 △ .
(1)求 的值;
(2)直接写出线段 , 的长(用含 的式子表示);
(3)在系列 △ 中,探究下列问题:
①当 为何值时, △ 是等腰直角三角形?
②设 , 均为正整数),问:是否存在 △ 与 △ 相似?若存在,求出其相似比;若不存在,说明理由.
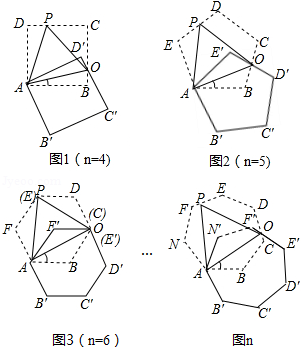
如图,将正 边形绕点 顺时针旋转 后,发现旋转前后两图形有另一交点 ,连接 ,我们称 为"叠弦";再将"叠弦" 所在的直线绕点 逆时针旋转 后,交旋转前的图形于点 ,连接 ,我们称 为"叠弦角", 为"叠弦三角形".
[探究证明]
(1)请在图1和图2中选择其中一个证明:"叠弦三角形" 是等边三角形;
(2)如图2,求证: .
[归纳猜想]
(3)图1、图2中的"叠弦角"的度数分别为 , ;
(4)图 中,"叠弦三角形" 等边三角形(填"是"或"不是"
(5)图 中,"叠弦角"的度数为 (用含 的式子表示)