已知抛物线
．
(1)试说明：无论m为何实数，该抛物线与x轴总有两个不同的交点；
(2)如图，当该抛物线的对称轴为直线x=3时，抛物线的顶点为点C，直线y=x－1与抛物线交于A、B两点，并与它的对称轴交于点D．
①抛物线上是否存在一点P使得四边形ACPD是正方形？若存在，求出点P的坐标；若不存在，说明理由；
②平移直线CD，交直线AB于点M，交抛物线于点N，通过怎样的平移能使得C、D、M、N为顶点的四边形是平行四边形．
解下列方程：(x＋3)2＝2x＋30．
（本题12分）如图，∠AOB为直角，∠BOC为锐角，且OM平分∠AOC，ON平分∠BOC．⑴若∠BOC＝50°，试求∠MON的度数；
⑵如果⑴中的∠BOC＝α（α为锐角），其
他条件不变，试求∠MON的度数；⑶如果⑴中∠AOB＝β，其他条件不变，你能求出∠MON的度数吗？
⑷从⑴⑵⑶的结果，你能看出什么规律？
．（本题10分）为了防控冬季呼吸道疾病，某校积极进行校园环境消毒工作，购买了 甲、乙两种消毒液共80瓶，其中甲种每瓶6元，乙种每瓶8元，如果购买这两种消毒液共花去500元，求甲、乙两种消毒液各购买
了多少瓶？
（本题 8 分）两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是40千米/时,水流速度是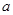
千米/时.2小时后, 乙船比甲船少航行多少千米?
（本题 8 分）一个角的余角与这个角的3倍互补，求这个角的度数．