某工厂有一种材料，可加工甲、乙、丙三种型号机械配件共240件，厂方计划由20个工人一天内加工完成，并要求每人只加工一种配件，根据下表提供的信息，解答下列问题：
| 配件种类 |
甲 |
乙 |
丙 |
| 每人可加工配件的数量（个） |
16 |
12 |
10 |
| 每个配件获利（元） |
6 |
8 |
5 |
（1）设加工甲种配件的人数为x，加工乙种配件的人数为y，求y与x之间的函数关系式
（2）如果加工每种配件的人数均不少于3人，那么加工配件的人数安排方案有几种？并写出每种安排方案
（3）要使此次加工配件的利润最大，应采用哪种方案？最大利润是多少？
（1）如图1，4条直线l1、l2、l3、l4是一组平行线，相邻2条平行线的距离都是2cm，正方形ABCD的4个顶点A、B、C、D分别在l1、l3、l4、l2上，求该正方形的面积；
（2）如图2，把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中，恰好四个顶点都在横格线上，已知∠1=36°，求长方形卡片的周长．（精确到1mm）（参考数据：sin36°≈0．60，cos36°≈0．80，tan36°≈0．75）
（1）如图1，已知⊙O的半径是4，△ABC内接于⊙O，AC=4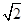
．
①求∠ABC的度数；
②已知AP是⊙O的切线，且AP=4，连接PC．判断直线PC与⊙O的位置关系，并说明理由；
（2）如图2，已知▱ABCD的顶点A、B、D在⊙O上，顶点C在⊙O内，延长BC交⊙O于点E，连接DE．求证：DE=DC．
从南京站开往上海站的一辆和谐号动车，中途只停靠苏州站，甲、乙、丙3名互不相识的旅客同时从南京站上车．
（1）求甲、乙、丙三名旅客在同一个站下车的概率；
（2）求甲、乙、丙三名旅客中至少有一人在苏州站下车的概率．
（1）解不等式组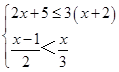
；
（2）先化简，再求值：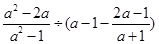
，其中a是方程x2+x=6的一个根．
（1）计算：-32+（1-π）0+（-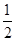
）-2；
（2）因式分解：3x2y-18xy2+27y3．