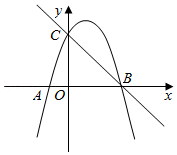
（11·西宁）（本小题满分12分）在平面直角坐标系中，现将一-优题课

（11·西宁）（本小题满分12分）在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C为 (－1，0)．如图17所示，B点在抛物线图象上，过点B作BD⊥x轴，垂足为D，且B点横坐标为－3．
（1）求证：△BDC≌△COA；
（2）求BC所在直线的函数关系式；
（3）抛物线的对称轴上是否存在点P，使△ACP是以AC为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．

科目数学题型解答题难度中等

知识点：三角形的五心二次函数在给定区间上的最值

为了提高学生体质，战胜疫情，某中学组织全校学生宅家一分钟跳绳比赛，全校跳绳平均成绩是每分钟99次，某班班长统计了全班50名学生一分钟跳绳成绩，列出的频数分布直方图如图所示，（每个小组包括左端点，不包括右端点）．

求：（1）该班一分钟跳绳的平均次数至少是多少，是否超过全校的平均次数；

（2）该班的一个学生说：“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围；

（3）从该班中任选一人，其跳绳次数超过全校平均数的概率是多少．

如图，已知二次函数 $y = - x^{2} + bx + c$ 的图象经过点 $A (- 1, 0)$ ， $B$ $(3, 0)$ ，与 $y$ 轴交于点 $C$ ．

（1）求抛物线的解析式；

（2）抛物线上是否存在点 $P$ ，使 $∠ PAB = ∠ ABC$ ，若存在请直接写出点 $P$ 的坐标．若不存在，请说明理由．

如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中， $ΔABC$ 的三个顶点 $A (5, 2)$ 、 $B (5, 5)$ 、 $C (1, 1)$ 均在格点上．

（1）将 $ΔABC$ 向左平移5个单位得到△ $A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

（2）画出△ $A_{1} B_{1} C_{1}$ 绕点 $C_{1}$ 顺时针旋转 $90 °$ 后得到的△ $A_{2} B_{2} C_{1}$ ，并写出点 $A_{2}$ 的坐标；

（3）在（2）的条件下，求△ $A_{1} B_{1} C_{1}$ 在旋转过程中扫过的面积（结果保留 $π)$ ．

先化简，再求值： $(2 - \frac{x - 1}{x + 1}) \div \frac{x^{2} + 6 x + 9}{x^{2} - 1}$ ，其中 $x = 3 \tan 30 ° - 3$ ．

如图，已知直线 $AB$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，线段 $OA$ 的长是方程 $x^{2} - 7 x - 18 = 0$ 的一个根， $OB = \frac{1}{2} OA$ ．请答案下列问题：

（1）求点 $A$ ， $B$ 的坐标；

（2）直线 $EF$ 交 $x$ 轴负半轴于点 $E$ ，交 $y$ 轴正半轴于点 $F$ ，交直线 $AB$ 于点 $C$ ．若 $C$ 是 $EF$ 的中点， $OE = 6$ ，反比例函数 $y = \frac{k}{x}$ 图象的一支经过点 $C$ ，求 $k$ 的值；

（3）在（2）的条件下，过点 $C$ 作 $CD ⊥ OE$ ，垂足为 $D$ ，点 $M$ 在直线 $AB$ 上，点 $N$ 在直线 $CD$ 上．坐标平面内是否存在点 $P$ ，使以 $D$ ， $M$ ， $N$ ， $P$ 为顶点的四边形是正方形？若存在，请写出点 $P$ 的个数，并直接写出其中两个点 $P$ 的坐标；若不存在，请说明理由．

试卷网试题网古诗词网作文网范文网