(11·西宁)(本小题满分10分)已知:如图,BD为⊙O的直径,AB=AC,AD交BC与E,AE=2,ED=4.
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使BF=OB,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
(·黑龙江省黑河市、齐齐哈尔市、大兴安岭)【8分】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
(·黑龙江哈尔滨)(本题8分)
如图1, 平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).

(·辽宁葫芦岛)在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.
(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;
(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,
(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.
(·辽宁沈阳)如图,点E为矩形ABCD外一点,AE=DE,连接EB、EC分别与AD相交于点F、G.
求证:(1)△EAB≌△EDC;
(2)∠EFG=∠EGF.
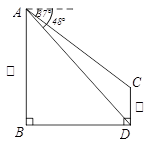
(·辽宁丹东)23.如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.