(成都)(本小题满人8分)国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步晋及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)求获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用树状图或列表的方法求恰好达到A,B两所学校的概率.
有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b写出k为负数的概率

2010年4月14日清晨7时49分,青海玉树发生了7.1级强烈地震,伤亡巨大,损伤惨重.某市某中学某班为灾区献爱心的捐款活动进行了抽样调查,结果如图所示.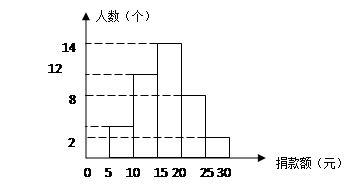
若捐款在10~15元的频率为0.3,则捐款额在10元以下的学生有多少人?
若从中任意抽取一位同学,则该同学的捐款额在15元以上的概率是多少?
若该校共有学生1600人,估计全校学生一共捐款多少元?
下图是一座人行天桥的示意图,天桥的高是10米,坡面的倾斜角为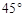 .为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为
.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为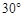 ,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?
,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?
为推动青少年学生“阳光体育”运动,我省今年中考体育学科为30分,成绩记入考试总分. 某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按 四个等级进行统计,并将结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:
四个等级进行统计,并将结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:
(其中:A级:25~30分;B级:21~24分;C级:18~20分;D级:18分以下)求出扇形统计图中C级所在的扇形圆心角的度数
该班学生体育测试成绩的中位数落在哪个等级内;
若该校九年级学生共有600人,请你估计这次考试中A级和B级的学生共有多少人?
受金融危机的影响,某厂家生产的电器出现了滞销情况,为促进销售,这种电器经过连续两次降价,利润由800元下降到344元.已知降价前该商品的利润率是50%,如果两次降价的百分率一样,求每次降价的百分率.(商品利润率= )
)