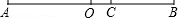(11·西宁)(本小题满分12分)在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0).如图17所示,B点在抛物线 图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
画出数轴,并在数轴上表示下列各数,并比较这五个数的大小(用“<”连接).﹣5,2,﹣ ,﹣2.5,0.
,﹣2.5,0.
某校学生列队以8千米/时的速度前进,在队尾,校长让一名学生跑步到队伍的最前面找带队老师传达一个指示,然后立即返回队尾,这位学生的速度是12千米/时,从队尾出发赶到排头又回队尾共用了3.6分钟,求学生队伍的长.
考考你的应用能力周末,七年级一班准备邀请所有教师14人和全班48名同学去公园举行游园活动,已知公园有两种售票方式:①成人票8元/人,学生票5元/人;②团体票统一按成人票的7折计算(50人以上可买团体票).
(1)若师生均到齐,选用哪种方式购票较合算?
(2)若教师没有到齐,用第二种购票方式共需336元,你能算出有几位教师没有到吗?
如图,已知∠AOB=50°,∠BOC=90°,OM、ON分别是∠AOB、∠BOC的角平分线,求∠MON的度数.
如图:线段AB=14cm,C是AB上一点,且AC=9cm,O是AB的中点,求线段OC的长度.