图甲是一个水桶模型示意图，水桶提手结构的平面图是轴对称图形.当点O到BC（或DE）的距离大于或等于⊙O的半径时（⊙O是桶口所在圆，半径为OA），提手才能从图甲的位置转到图乙的位置，这样的提手才合格.现用金属材料做了一个水桶提手（如图丙A-B-C-D-E-F，C-D是
，其余是线段），O是AF的中点，桶口直径AF =34cm，AB=FE=5cm，∠ABC =∠FED =149°.请通过计算判断这个水桶提手是否合格.
（参考数据：
≈17.72，tan73.6°≈3.40，sin75.4°≈0.97.）
 |
已知：如图，在等腰梯形ABCD中，AB//CD，点E、F分别在AD、BC上，且DE＝CF．
求证：AF＝BE
解不等式组：
解方程：
如图1，在直角坐标系中，已知点A（0，2）、点B（－2，0），过点B和线
段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE.
（1）填空：点D的坐标为（），点E的坐标为（）.
（2）若抛物线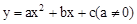
经过A、D、E三点，求该抛物线的解析式.
（3）若正方形和抛物线均以每秒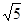
个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E
落在y轴上时，正方形和抛物线均停止运动.
①在运动过程中，设正方形落在y轴右侧部分的面积为s，求s关于平移时间t（秒）的函数关系式，
并写出相应自变量t的取值范围.
②运动停止时，求抛物线的顶点坐标.
如图，C是以AB为直径的⊙O上一点，过O作OE⊥AC于点E，过点A作
⊙O的切线交OE的延长线于点F，连结CF并延长交BA的延长线于点P.
（1）求证：PC是⊙O的切线.
（2）若AF=1，OA=
，求PC的长. 