初中生对待学习的态度一直是教育工作者关注的问题之一.为此菏泽市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
某市现有两种用电收费方法:
| 分时电表 |
普通电表 |
|
| 峰时(8:00—21:00) |
谷时(21:00到次日8:00) |
电价0.52元/度 |
| 电价0.55元/度 |
电价0.35元/度 |
小明家所在的小区的电表都换成了分时电表,根据情况回答下列问题:
(1)第一季度小明家用电情况为:谷时用电量100度,峰时用电量300度,这个季度的费用和用普通电表收费相比,哪种收费方法合算?试说明理由.
(2)一月份小明家用电100度,那么小明家使用分时电表是不是一定比普通电表合算?试说明理由.
如图,△ABC为等边三角形,E为AC上一点,连接BE,将△BEC旋转,使点C落在BC上的点D处,点B落在BC上方的点F处,点E落在点C处,连接AF.求证:四边形ABDF为平行四边形.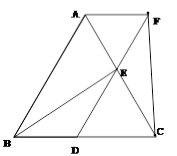
某文具店老板第一次用1000元购进一批文具,很快销售完毕,第二次购进时发现每件文具的进价比第一次上涨了2.5元,老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,已知两批文具的售价均为每件15元.
(1)第二次购进了多少件文具?
(2)文具店老板在这两笔生意中共盈利多少元?
如图,在△ABC中,∠B =" 64" °,∠BAC =" 72" °,D为BC上一点 ,DE交AC于点F,且AB=AD=DE,连接AE,∠E=55°,请判断△AFD的形状,并说明理由.
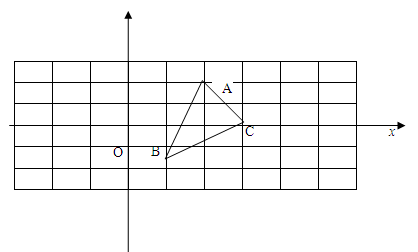
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).
(1)画出△ABC关于x轴对称的△A’B’C’,并求出点A’、B’、C’的坐标.
|
(2)在坐标平面内是否存在点D,使得△COD为等腰三角形?若存在,直接写出点D的坐标(找出满足条件的两个点即可),若不存在,请说明理由.