如图,小明在大楼30米高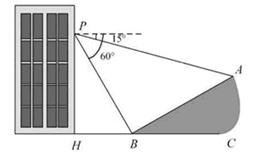
(即PH=30米)的窗口P处进行观测,测得山
坡上A处的俯角为15°,山脚B处的俯角为
60°,已知该山坡的坡度i(即tan∠ABC)为1: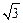 ,点P、H、B、C、A在同一个平面上.点
,点P、H、B、C、A在同一个平面上.点
H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 ▲ 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: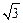 ≈1.732).
≈1.732).
(本题10分)如图,抛物线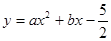 经过A(﹣1,0),B(5,0)两点.
经过A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
(本题8分)某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量 与销售单价
与销售单价 之间的关系可以近似地看作一次函数:
之间的关系可以近似地看作一次函数: ,物价部门规定这种笔记本每本的销售单价不得高于18元.
,物价部门规定这种笔记本每本的销售单价不得高于18元.
(1)当每月销售量为70本时,获得的利润为多少元?
(2)该文具店这种笔记本每月获得利润为 元,求每月获得的利润
元,求每月获得的利润 元与销售单价
元与销售单价 之间的函数关系式,并写出自变量的取值范围.
之间的函数关系式,并写出自变量的取值范围.
(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
(本题8分)如图AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连结AC、OC、BC.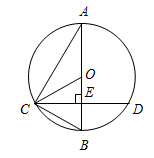
(1)求证:∠ACO=∠BCD;
(2)若EB=2cm,CD=8m,求⊙O的直径.
(本题8分)一个不透明的布袋里装有4个球,其中3个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球.求两次摸出的球恰好颜色相同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为 ,求n的值.
,求n的值.
(本题6分)已知二次函数的图象以 为顶点,且过点
为顶点,且过点 .
.
(1)求该二次函数的解析式;
(2)求该二次函数图象与坐标轴的交点坐标;