如图1，Rt△ABC两直角边的边长为AC＝1，BC＝2．
（1）如图2，
⊙O与Rt△ABC的边AB相切于点X，与边CB相切于点Y．请你在图2中作出并标明⊙O的圆心O；（用尺规作图，保留作图痕迹，不写作法和证明）
（2）P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切．设⊙P的面积为s，你认为能否确定s的最大值？若能，请你
求出s的最大值;若不能,请你说明不能确定s的最大值的理由．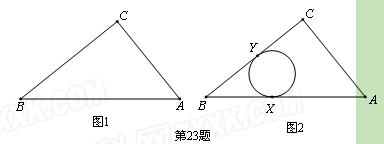
解不等式组
．
解方程：
．
如图
，已知抛物线过点A（0，6），B（2，0），C（7，
）．
（1）求抛物线的解析式；
（2）若D是抛物线的顶点，E是抛物线的对称轴与直线AC的交点，F与E关于D对称，求证：∠CFE=∠AFE；
（3）在y轴上是否存在这样的点P，使△AFP与△FDC相似，若有请求出所有和条件的点P的坐标，若没有，请说明理由．
已知△ABC，分别以AC和BC为直径作半圆O1，O2，P是AB的中点，
（1）如图1，若△ABC是等腰三角形，且AC=BC，在
，
上分别取点E、F，使∠AO1E=∠BO2F
，则有结论①△PO1E≌△FO2P，②四边形PO1CO2是菱形，请给出结论②的证明；
（2）如图2，若（1）中△ABC是任意三角形，其他条件不变，则（1）中的两个结论还成立吗？若成立，请给出证明；
（3）如图3，若PC是⊙O1的切线，求证：AB2=BC2+3AC2．
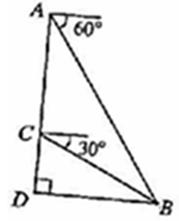
青青草原上，灰太狼每天都想着如何抓羊，而且是屡败屡试，永不言弃．（如图所示）一天，灰太狼在自家城堡顶部A处观察羊羊们时，发现懒洋洋在大树底下睡懒觉，此时，测得懒洋洋所在地B处的俯角为60°，然后下到城堡的C处，测得B处的俯角为30°．已知AC=40米，若灰太狼以5m/s的速度从城堡底部D处出发，几秒种后能抓到懒羊羊？（结果精确到个位）．