(本小题满分12分)已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| |
甲 |
乙 |
丙 |
| 维生素A(单位/千克) |
600 |
700 |
400 |
| 维生素B(单位/千克) |
800 |
400 |
500 |
| 成本(元/千克) |
11 |
9 |
4 |
(Ⅰ)用x,y表示混合食物成本c元;
(Ⅱ)确定x,y,z的值,使成本最低.
一个袋子中装有6个红球和4个白球,假设袋子中的每一个球被摸到可能性是相等的。
(Ⅰ)从袋子中任意摸出3个球,求摸出的球均为白球的概率;
(Ⅱ)一次从袋子中任意摸出3个球,若其中红球的个数多于白球的个数,则称“摸球成功”(每次操作完成后将球放回),某人连续摸了3次,记“摸球成功”的次数为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
已知函数 .
.
(Ⅰ)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)已知 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值.
(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
已知动点 到直线
到直线
 的距离是它到点
的距离是它到点 的距离的
的距离的 倍.
倍.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设轨迹 上一动点
上一动点 满足:
满足: ,其中
,其中 是轨迹
是轨迹 上的点,直线
上的点,直线 与
与 的斜率之积为
的斜率之积为 ,若
,若 为一动点,
为一动点, 为两定点,
为两定点, .
.
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
已知一家公司生产某种品牌服装的年固定成本为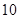 万元,每生产
万元,每生产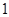 千件需另投入
千件需另投入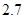 万元.设该公司一年内生产该品牌服装
万元.设该公司一年内生产该品牌服装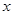 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为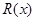 万元,且
万元,且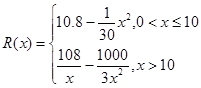
(Ⅰ)写出年利润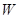 (万元)关于年产量
(万元)关于年产量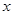 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大年利润.(注:年利润=年销售收入-年总成本).
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
在如图所示的多面体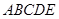 中,
中,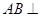 平面
平面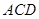 ,
, 平面
平面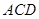 ,
,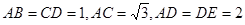 ,
,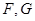 为
为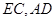 的中点.
的中点.
(Ⅰ)求证: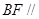 平面
平面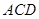 ;
;
(Ⅱ)求三棱锥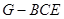 的体积.
的体积.