在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为 ;小红在剩下有三个小球中随机取出一个小球,记下数字
;小红在剩下有三个小球中随机取出一个小球,记下数字 。
。
(1)计算由 、
、 确定的点(
确定的点( ,
, )在函数
)在函数 图象上的概率;
图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若 、
、 满足
满足 ,则小明胜;若
,则小明胜;若 、
、 满足
满足 ,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
如图,抛物线y=-x2+(m+2)x-3(m-1)交x轴于A、B,交y轴于C.直线y=(m+1)x-3经过点A.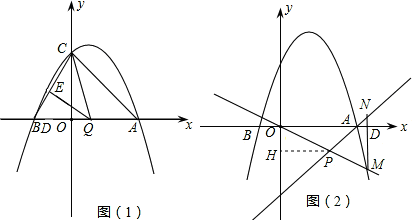
(1)求抛物线的解析式;
(2)点Q为线段AB上的动点,过点Q作QE∥AC,交BC于E,连CQ.当S△CQE的面积最大时,求点Q的坐标;
(3)直线y=kx(k<0)交直线y=(m+1)x-3于P,交抛物线y=-x2+(m+2)x-3(m-1)于点M,过M作x轴的垂线,垂足为D,交直线y=(m+1)x-3于N.△PMN能否为等腰三角形?若能,求k的值;若不能,说明理由.
红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
时间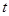 (天) (天) |
1 |
3 |
5 |
10 |
36 |
… |
| 日销售量m(件) |
94 |
90 |
86 |
76 |
24 |
… |
未来40天内,前20天每天的价格 (元/件)与时间
(元/件)与时间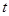 (天)的函数关系式为
(天)的函数关系式为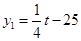 (
( 且
且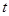 为整数),后20天每天的价格
为整数),后20天每天的价格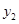 (元/件)与时间
(元/件)与时间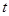 (天)的函数关系式为
(天)的函数关系式为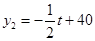 (
(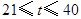 且
且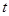 为整数).
为整数).
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与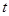 (天)之间的关系式;
(天)之间的关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠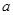 元利润(
元利润(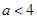 )给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间
)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间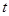 (天)的增大而增大,求
(天)的增大而增大,求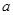 的取值范围.
的取值范围.
如图,在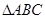 中,
中,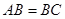 .以AB为直径作圆⊙O交AC于点D,点E为⊙O上的一点,连接ED并延长与BC的延长线交于点F.连接AE、BE,∠BAE=60°,∠F=15°,解答下列问题.
.以AB为直径作圆⊙O交AC于点D,点E为⊙O上的一点,连接ED并延长与BC的延长线交于点F.连接AE、BE,∠BAE=60°,∠F=15°,解答下列问题.
(1)求证:直线FB是⊙O的切线;
(2)若BE=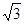 cm,求AC的长.
cm,求AC的长.
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1: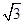 (即AB:BC=1:
(即AB:BC=1: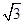 ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).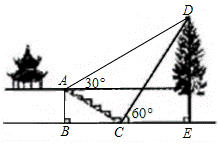
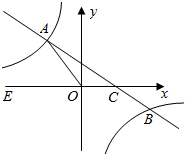
如图,在平面直角坐标系xoy中,一次函数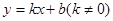 的图象与反比例函数
的图象与反比例函数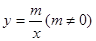 的图象交于二、四象限内的A、B两点,与x轴交于C点,点B坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
的图象交于二、四象限内的A、B两点,与x轴交于C点,点B坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE= 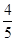 .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
(3)直接写出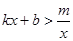 时的x取值范围.
时的x取值范围.