已知函数 的图象经过点
的图象经过点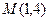 ,曲线在点
,曲线在点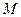 处的切线恰好与
处的切线恰好与
直线 垂直.
垂直.
(1)求实数 的值;
的值;
(2)若函数 在区间
在区间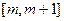 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
在1,2,3,…,100中任意取三个数字构成等差数列,有几种不同的排法?
如图,直线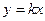 分抛物线
分抛物线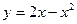 与
与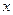 轴所围图形为面积相等的两部分,求实数
轴所围图形为面积相等的两部分,求实数 的值.
的值.
(本题满分18分;第(1)小题4分,第(2)小题6分,第(3)小题8分)
设数列 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列 中任意(不同)两项之和仍是该数列中的一项,则
中任意(不同)两项之和仍是该数列中的一项,则 称该数列是“封闭数列”.
称该数列是“封闭数列”.
(1)若 ,判断该数列是否为“封闭数列”,并说明理由?
,判断该数列是否为“封闭数列”,并说明理由?
(2)设 是数列
是数列 的前
的前 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存
;若存 在,求
在,求 的通项公式,若不存在,说明理由;
的通项公式,若不存在,说明理由;
(3)试问:数列 为“封闭数列”的充要条件是什么?给出你的结论并加以证明.
为“封闭数列”的充要条件是什么?给出你的结论并加以证明.
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设 、
、 为坐标平面
为坐标平面 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点 (异于
(异于 ).
).
(1)若对任意
 ,点
,点 在抛物线
在抛物线 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2)若点 在椭圆
在椭圆 上,试问:点
上,试问:点 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3)对(1)中点 所在圆方程
所在圆方程 ,设
,设 、
、 是圆
是圆 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 相切.
相切.
(满分16分;第(1)小题5分,第(2)小题5分,第三 小题6分)
小题6分)
已知函数 
(1)判断并证明 在
在 上的单调性;
上的单调性;
(2)若存在 ,使
,使 ,则称
,则称 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值,并求出不动点
的值,并求出不动点 ;
;
(3)若 在
在 上恒成立 , 求
上恒成立 , 求 的取值范围.
的取值范围.