（本题满分18分；第（1）小题4分，第（2）小题6分，第（3）小题8分）
设数列
是等差数列，且公差为
，若数列
中任意（不同）两项之和仍是该数列中的一项，则
称该数列是“封闭数列”.
（1）若
，判断该数列是否为“封闭数列”，并说明理由？
（2）设
是数列的前
项和，若公差
，试问：是否存在这样的“封闭数列”，使
；若存
在，求的通项公式，若不存在，说明理由；
（3）试问：数列为“封闭数列”的充要条件是什么？给出你的结论并加以证明.
（本小题满分13分）
在平面直角坐标系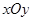
中，已知点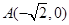
，
，
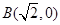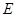为动点，且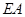直线
与直线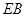
的斜率之积为
．
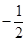（Ⅰ）求动点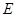的轨迹
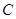的方程；
（Ⅱ）设过点
的直线
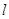与曲线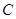相交于不同的两点
，
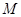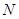．若点
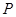在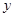
轴上，且<满足
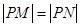，求点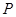的纵坐标的取值范围．
（本小题满分14分）
已知函数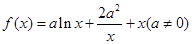
．
（Ⅰ）若曲线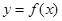
在点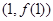
处的切线与直线
垂直，求实数
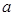的值；
（Ⅱ）讨论函数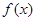
的单调性；
（Ⅲ）当
时，记函数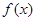的最小值为
，求证：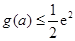
．
（本小题满分14分）
在如图所示的几何体中，四边形
为正方形，
平面，
，
．
（Ⅰ）若点
在线段
上，且满足
,求证：
平面
；
（Ⅱ）求证：
平面
；
（Ⅲ）求二面角
的余弦值．
（本小题满分13分）
一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球，从中任意取出3个球．
（Ⅰ）求取出的3个球颜色相同且编号是三个连续整数的概率；
（Ⅱ）求取出的3个球中恰有2个球编号相同的概率；
（Ⅲ）记X为取出的3个球中编号的最大值，求X的分布列与数学期望．
（本小题满分13分）
已知函数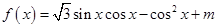
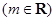的图象过点
．
（Ⅰ）求
的值；
（Ⅱ）在△
中，角
，
，
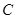的对边分别是
，
，
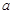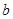．若
，求
的取值范围．