如图,已知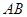 ⊥平面
⊥平面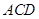 ,
,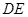 ∥
∥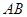 ,
,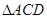 是正三角形,
是正三角形,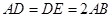 ,且
,且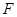 是
是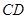 的中点.
的中点.
(Ⅰ)求证: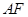 ∥平面
∥平面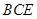 ;
;
(Ⅱ)求证:平面BCE⊥平面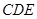 .
.
设函数f(x)=sin x+sin .
.
(1)求f(x)的最小值,并求使f(x)取得最小值的x的集合;
(2)不画图,说明函数y=f(x)的图像可由y=sin x的图像经过怎样的变化得到.
如图1,A,D分别是矩形A1BCD1上的点,AB=2AA1=2AD=2,DC=2DD1,把四边形A1ADD1沿AD折叠,使其与平面ABCD垂直,如图2所示,连接A1B,D1C得几何体ABA1DCD1.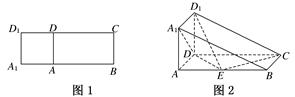
(1)当点E在棱AB上移动时,证明:D1E⊥A1D;
(2)在棱AB上是否存在点E,使二面角D1ECD的平面角为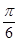 ?若存在,求出AE的长;若不存在,请说明理由.
?若存在,求出AE的长;若不存在,请说明理由.
如图,在四棱锥PABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2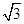 ,E是PB上任意一点.
,E是PB上任意一点.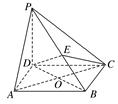
(1)求证:AC⊥DE;
(2)已知二面角APBD的余弦值为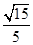 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.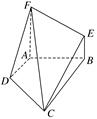
(1)证明:在平面BCE上,一定存在过点C的直线l与直线DF平行;
(2)求二面角FCDA的余弦值.
如图,在四棱锥PABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=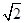 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.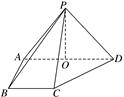
(1)求直线PB与平面POC所成角的余弦值;
(2)求B点到平面PCD的距离;
(3)线段PD上是否存在一点Q,使得二面角QACD的余弦值为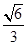 ?若存在,求出
?若存在,求出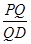 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.