如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.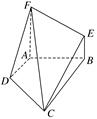
(1)证明:在平面BCE上,一定存在过点C的直线l与直线DF平行;
(2)求二面角FCDA的余弦值.
解关于的不等式: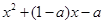 <
< .
.
如图是一个从 的”闯关”游戏.
的”闯关”游戏. 
规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于 则闯关成功.
则闯关成功.
(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望。
如图所示,在三棱锥PABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.
(1)求证:AB⊥平面PBC;
(2)设AB=BC,直线PA与平面ABC所成的角为45°,求异面直线AP与BC所成的角;
(3)在(2)的条件下,求二面角C-PA-B的余弦值.
已知 的展开式前三项中的
的展开式前三项中的 的系数成等差数列.
的系数成等差数列.
(1)展开式中所有的 的有理项为第几项?
的有理项为第几项?
(2)求展开式中系数最大的项.
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
| 患病 |
未患病 |
总计 |
|
| 没服用药 |
20 |
30 |
50 |
| 服用药 |
x |
y |
50 |
| 总计 |
M |
N |
100 |
设从没服用药的动物中任取两只,未患病数为X;从服用药物的动物中任取两只,未患病数为Y,工作人员曾计算过P(X=0)= P(Y=0).
P(Y=0).
(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次, 若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为 .,求
.,求 的期望E(
的期望E( )和方差D(
)和方差D( ).
).
参考公式: (其中
(其中 )
)
| P(K2≥k) |
0.25 |
0.15 |
0.10 |
0.05 |
0.010 |
0.005 |
| k |
1.323 |
2.072 |
2.706 |
3.845 |
6.635 |
7.879 |