如图是一个从 的”闯关”游戏.
的”闯关”游戏. 
规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于 则闯关成功.
则闯关成功.
(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望。
已知向量
 ,
,
 ,
,
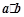
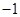 .
.
(1)求函数 的单调递减区间及其图象的对称轴方程;
的单调递减区间及其图象的对称轴方程;
(2)当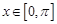 时,若
时,若 ,求
,求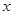 的值.
的值.
(本小题满分14分)若存在实常数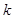 和
和 ,使得函数
,使得函数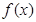 和
和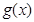 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和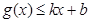 ,则称直线
,则称直线 为
为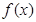 和
和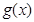 的“隔离直线”.已知
的“隔离直线”.已知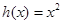 ,
, 为自然对数的底数).
为自然对数的底数).
(1)求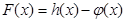 的极值;
的极值;
(2)函数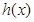 和
和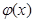 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
(本小题满分12分)杭州某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔腾6号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题:
(1)引进该设备多少年后,开始盈利?
(2)引进该设备若干年后,有两种处理方案:
第一种:年平均盈利达到最大值时,以26万元的价格卖出;
第二种:盈利总额达到最大值时,以8万元的价格卖出.
哪一种方案较为合算?请说明理由.
(本小题满分12分)在如图所示的几何体中,面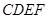 为正方形,面
为正方形,面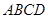 为等腰梯形,
为等腰梯形,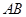 //
//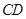 ,
,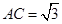 ,
, ,
, .
.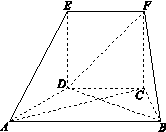
(1)求证: 平面
平面 ;
;
(2)求四面体 的体积;
的体积;
(2)线段 上是否存在点
上是否存在点 ,使
,使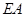 //平面
//平面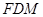 ?证明你的结论.
?证明你的结论.
(本小题满分12分)数列 满足
满足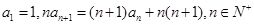
(1)证明:数列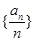 是等差数列;
是等差数列;
(2)设 ,求数列
,求数列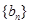 的前
的前 项和
项和