（本题8分）某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个，且制成一个甲盒比制作一个乙盒需要多用20%的材料。
（1）求制作每个甲盒、乙盒各用多少材料？
（2）如果制作甲、乙两种包装盒3000个，且甲盒的数量不少于乙盒数量的2倍，那么请写出所需材料总长度
与甲盒数量
之间的函数关系式，并求出最少需要多少米材料。
如图，边长为2的正方形ACDE所在的平面与平面ABC垂直，AD与CE的交点为M，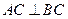
，且AC=BC.
（1）求证：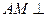
平面EBC；
（2求二面角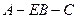
的大小.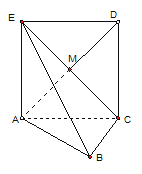
已知空间三点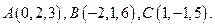
（1）求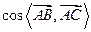
（2）求以AB，AC为边的平行四边形
的面积。
（本小题满分14分）
若函数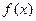
满足：对定义域内任意两个不相等的实数
,都有，则称函数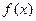为H函数.已知
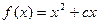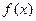,且为偶函数.
(1) 求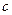
的值；
(2) 求证: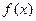为H函数；
(3)试举出一个不为H函数的函数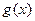
,并说明理由.
（本小题满分14分）
已知函数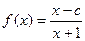
, 其中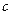
为常数，且函数
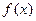图像过原点.
(1)求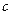的值；
(2)证明函数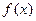在[0,2]上是单调递增函数；
(3)已知函数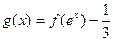
, 求函数
的零点
（本小题满分12分）
如图：A、B两城相距100 km，某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气. 已知D地距A城x km，为保证城市安全，天燃气站距两城市的距离均不得少于10km . 已知建设费用y (万元)与A、B两地的供气距离(km)的平方和成正比，当天燃气站D距A城的距离为40km时, 建设费用为1300万元.（供气距离指天燃气站距到城市的距离）
（1）把建设费用y(万元)表示成供气距离x (km)的函数，并求定义域；
（2）天燃气供气站建在距A城多远，才能使建设供气费用最小.，最小费用是多少？