如图，在四棱锥PABCD中，侧面PAD⊥底面ABCD，侧棱PA＝PD＝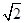
，PA⊥PD，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AB＝BC＝1，O为AD中点．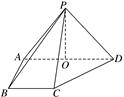
(1)求直线PB与平面POC所成角的余弦值；
(2)求B点到平面PCD的距离；
(3)线段PD上是否存在一点Q，使得二面角QACD的余弦值为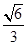
？若存在，求出
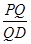的值；若不存在，请说明理由．
如图，圆O是等腰三角形ABC的外接圆，AB＝AC，延长BC到点D，使CD＝AC，连结AD交圆O于点E，连结BE与AC交于点F.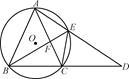
(1)判断BE是否平分∠ABC，并说明理由；
(2)若AE＝6，BE＝8，求EF的长．
如图所示，圆O的两弦AB和CD交于点E，EF∥CB，EF交AD的延长线于点F，FG切圆O于点G.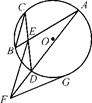
(1)求证：△DEF∽△EFA；
(2)如果FG＝1，求EF的长．
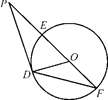
如图，圆O的直径AB的延长线与弦CD的延长线相交于点P，E为圆O上一点，AE＝AC，求证：∠PDE＝∠POC.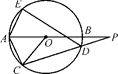
如图，AB是圆O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F.求证：∠DEA＝∠DFA.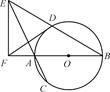
如图，已知P是圆O外一点，PD为圆O的切线，D为切点，割线PEF经过圆心O，若PF＝12，PD＝4
，求圆O的半径长和∠EFD的大小．