当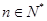 时
时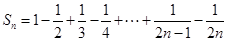 ,
,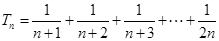
(1)求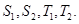
(2)猜想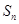 与
与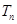 的关系,并用数学归纳法证明。
的关系,并用数学归纳法证明。
已知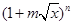 (
(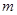 是正实数)的展开式的二项式系数之和为256,展开式中含
是正实数)的展开式的二项式系数之和为256,展开式中含 项的系数为112.
项的系数为112.
(1)求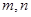 的值;
的值;
(2)求展开式中奇数项的二项式系数之和;
(3)求 的展开式中含
的展开式中含 项的系数.
项的系数.
(用数字作答)
4个男同学,3个女同学站成一排.
(1)男生甲必须排在正中间,有多少种不同的排法?
(2)3个女同学必须排在一起,有多少种不同的排法?
(3)任何两个女同学彼此不相邻,有多少种不同的排法?
(4)其中甲、乙两名同学之间必须有3人,有多少种不同的排法?
(用数字作答)
设实部为正数的复数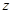 ,满足
,满足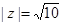 ,且复数
,且复数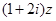 在复平面上对应的点在第一、三象限的角平分线上.
在复平面上对应的点在第一、三象限的角平分线上.
(1)求复数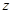 ;
;
(2)若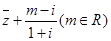 为纯虚数, 求实数
为纯虚数, 求实数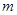 的值.
的值.
已知二次函数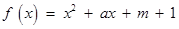 ,及函数
,及函数 。
。
关于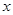 的不等式
的不等式 的解集为
的解集为 ,其中
,其中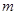 为正常数。
为正常数。
(1)求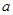 的值;
的值;
(2)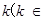 R
R 如何取值时,函数
如何取值时,函数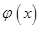
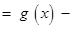
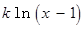 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且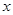
 ,求证:
,求证:
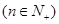 。
。
已知函数 ,
,
(1)若x=1时 取得极值,求实数
取得极值,求实数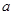 的值;
的值;
(2)当 时,求
时,求 在
在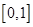 上的最小值;
上的最小值;
(3)若对任意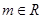 ,直线
,直线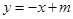 都不是曲线
都不是曲线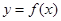 的切线,求实数
的切线,求实数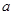 的取值范围。
的取值范围。