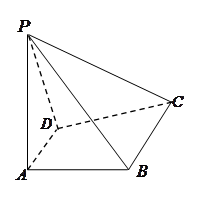
如图: PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面
PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF.
已知中心在原点,焦点在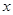 轴上的椭圆,离心率
轴上的椭圆,离心率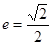 ,且经过抛物线
,且经过抛物线 的焦点.
的焦点.
(1)求椭圆的标准方程;
(2)若过点 的直线
的直线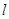 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点 (
( 在
在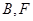
之间), 与
与 面积之比为
面积之比为 ,求
,求 的取值范围.
的取值范围.
已知函数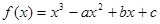 的图象为曲线C。
的图象为曲线C。
(1)若曲线C上存在点P,使曲线C在P点处的切线与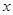 轴平行,求
轴平行,求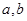 的关系;
的关系;
(2)若函数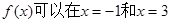 时取得极值,求此时
时取得极值,求此时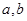 的值;
的值;
(3)在满足(2)的条件下,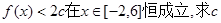 的取值范围。
的取值范围。
已知数列 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 ,数列
,数列 .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和Sn.
的前n项和Sn.
已知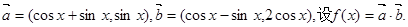
(1)求函数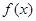 的最小正周期;
的最小正周期;
(2)当 的最大值及最小值。
的最大值及最小值。
如图,已知四棱锥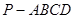 中,
中,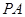 ⊥平面
⊥平面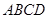 ,
, 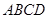 是直角梯形,
是直角梯形, ,
,
 90º,
90º,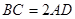 .
.
(1)求证: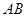 ⊥
⊥ ;
;
(2)在线段 上是否存在一点
上是否存在一点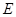 ,使
,使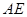 //平面
//平面 ,
,
若存在,指出点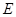 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.