把一个小球用细线悬挂起来,就成为单摆,摆长为L,最大偏角为θ,如果阻力可以忽略,小球运动到最低位置时的速度为多大?
如图所示为学校操场上一质量不计的竖直滑杆,滑杆上端固定,下端悬空,为了研究学生沿杆的下滑情况,在杆的顶部装有一拉力传感器,可显示杆顶端所受拉力的大小,现有一学生(可视为质点)从上端由静止开始滑下,5 s末滑到杆底时速度恰好为零,从学生开始下滑时刻计时,传感器显示拉力随时间变化情况如图所示,g取10 m/s2,求:
(1)该学生下滑过程中的最大速率;
(2)图中力F1的大小;
(3)滑杆的长度.
装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击.通过对以下简化模型的计算可以粗略说明其原因.
质量为2m、厚度为2d的钢板静止在水平光滑桌面上。质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿.现把钢板分成厚度均为d、质量均为m的相同两块,间隔一段距离平行放置,如图所示.若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度.设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞。不计重力影响。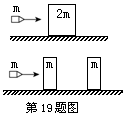
如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求:(1)木板第二次与墙碰撞前的速度;(2)木板从第一次与墙碰撞到再次碰撞所经历的时间。设木板足够长,重物始终在木板上.重力加速度为g。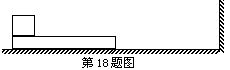
把地球上的一个秒摆(周期等于2s的摆称为秒摆)拿到月球上去,它的振动周期变为多少?已知地球质量M地=5.98×1024kg,半径R地=6.4×106m,月球质量M月=7.34×1022kg,半径R月=1.74×106m。(保留两位有效数字)
一质量为m=0.2kg的皮球。从高H=0.8m处自由落下,与地面相碰后反弹的最大高度为h=0.45m,则球与地面接触这段时间内皮球的动量的变化为多少?(g取10m/s2)